Understanding Non-Ergodic Processes and Its Implication in Various Fields
“Non ergodic” is a pivotal, yet often overlooked scientific term. To grasp its essence, one must first understand its counterpart: “ergodicity.” An “ergodic” system is one that eventually visits all its conceivable states. Think of a gas that is released into a controlled laboratory setting such as a glass box. When the system reaches equilibrium it is diffused throughout the box. Gas molecules are uniformly distributed at all points in space. An alternative way to view this experiment is to think in terms of time. Given enough time, the gas will be uniformly distributed throughout the glass box. Under conditions of equilibrium we can say that the distribution across time is aligned to the distribution across space. This allows us to adopt a simplified formula which can conveniently only consider the expectation value without worrying about the time dimension.
Rooted in Statistical Mechanics, this concept revolves around the “ergodic hypothesis,” a mathematical alternative to integrating Newton’s equations of motion for a system. Interestingly, ergodic systems don’t possess a deep-seated sense of “history.”
On the other hand, non-ergodic systems are quite the opposite. They don’t transition through every possible state. This difference carries profound implications.
Delving into the realm of biology, the evolution of life on Earth is undeniably non-ergodic and rich in history. Not every imaginable life form will emerge in our universe. This reality, combined with the phenomenon of heritable variation, sets the groundwork for Darwinian theory. While Darwin didn’t specify the exact methods of heritable variation, it’s pivotal to note that non-ergodicity shapes our historical narrative.
In equilibrium statistical mechanics, the ergodic hypothesis is invaluable. It predicates that the time average and the expectation value of an observable align. This hypothesis allows for complex dynamic descriptions to be simplified into probabilistic models, effectively side-lining the role of time. However, the scenarios where this assumption holds are limited, especially when dealing with systems that aren’t in equilibrium. This typically is found in many real world scenarios where systems evolve in time.
Surprisingly, economics, which frequently delves into non-equilibrium systems and growth models, has deeply entrenched itself in the ergodic assumption. Prevailing economic theories, such as expected utility theory and its successors, often make undiscriminating assumptions of ergodicity. The origins of this discrepancy trace back to the 17th-century when foundational ideas about risk and randomness in economics were formed. These concepts predated the introduction of ergodicity in 19th-century physics by a considerable margin.
Ole Peters and the Unveiling of Non-Ergodic Systems in Economics
Ole Peters is a luminary in highlighting the unique properties of non-ergodic systems, often challenging traditional views. His ground-breaking simulation involving a “gambling” game offers profound insights. Imagine starting with a bankroll of $100: every time you flip a coin and it lands on heads, you increase your bankroll by 50%. Conversely, flipping tails reduces it by 40%. To the casual observer, or someone steeped in traditional, ergodic thinking, this bet seems like a reasonable gamble. When one calculates expectations using a spatially weighted model, it does seem like a game with a small yet positive edge, especially as the game theoretically visits all states over countless trials.

The Famous Ole Peters Gambling Scenario¹
However, Peters’ simulation dismantled this perception. As he carried out his trials, a startling pattern emerged: regardless of the promising start, every wealth trajectory was plagued by an eventual risk of ruin. An unexpected force seemed to be at play, redirecting these trajectories. This force introduced the critical role of history or ‘time’ into determining the outcomes of his experiments.
The key to understanding this non-ergodic problem is to understand that the problem is an iterative problem dealing with non-linear (conditional) relations.
Imagine starting with a stake of $100. To accurately forecast its growth or decline, it’s essential to factor in this initial state when assigning probabilities. Say you hit a win, boosting your $100 to $150. However, if the next round results in a loss, your calculations shouldn’t merely deduct a fixed sum. Instead, they should reference the updated $150, resulting in a new total of $150 minus 40% of $150, which is $90.
This continuous consideration of the system’s preceding state, known as path dependence, is at the heart of the non-ergodic problem. It introduces cause and effect into the analysis of future paths. Ole Peters’ experiment illustrates this beautifully: by consistently referencing the system’s preceding state, we align with his outcomes. Those who overlook this pivotal step might mistakenly assume the game offers an advantageous edge.
Embracing path dependence reveals a startling insight: a system’s evolution isn’t bound to explore every conceivable state. Its trajectory is shaped, even dictated, by its historical states, making the past a powerful influencer of the future.
This particular experiment is now widely referenced as the “Ole Peters Gambling scenario.” It stands testament to the surprises non-ergodic systems can throw our way, challenging deeply-held beliefs in the financial and statistical worlds.
Given the intriguing results observed in certain simulations, it becomes pertinent to ask: what analytical tools are we employing to scrutinize financial markets? If these markets exhibit non-ergodic behaviours, are our tools adept enough? Are we inadvertently leaning on heuristic ergodic models that compute averages in a certain manner or models that assume results are independent to preceding causes? Or, are we embracing non-ergodic models that rightly acknowledge the crucial role of path dependence in determining outcomes?
The Enigma of Strange Attractors in Complex Adaptive Systems
Complex adaptive systems unlike simple games of chance also reveal peculiar path dependent properties when scrutinized over time. Specifically, in computer simulations that chart trajectories within a state space, not all potential states are reached. Instead, a peculiar entity, known as an “attractor,” emerges, influencing these trajectories and guiding them into a distinct geometry.
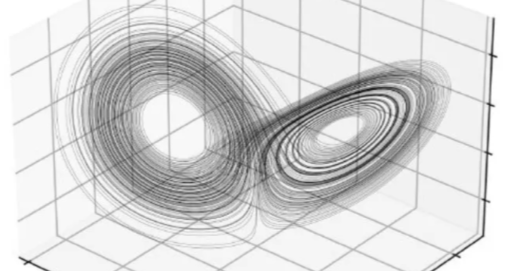
Lorentz stumbled upon this unique property while delving into chaos theory and studying the intertwining of periodicity with fractal geometry. The core mathematics involves the use of calculus to grasp properties of nonlinear differential equations.
The term “nonlinear” is paramount in this context. It describes systems in which inputs and outputs do not change proportionately. Financial markets, replete with numerous interconnected dependencies, are prime examples of such systems. The emotional response of humans offers a more intuitive example: winning $10 million in a lottery doesn’t generate ten times the excitement of winning $1 million.
Plotting trajectories of a set of nonlinear systems produces an unusual structure over time that restricts trajectories from exploring all possible states. These trajectories exhibit periods of predictability before making abrupt shifts to a different trajectory path with its own periodicity. Notably, the trajectory never circles back to its initiation point – a characteristic of non-ergodic systems, not ergodic ones. This emergent structure dominates the trajectory’s direction.

Unfolding of the Lorentz Attractor²
A parallel can be drawn with nonlinear systems like gravitational fields. For instance, an electron’s trajectory informs space on curving, but spacetime guides the electron’s motion. It’s a dance between micro and macro elements.
Regardless of the starting point in these simulations, trajectories eventually align, but never repeat, with a peculiar, dual-lobed shape. This spatial geometry, which asserts constraints on trajectory paths, is the “attractor.” They are ubiquitous in complex adaptive systems.
Continued simulations unravel the full splendor of this structure, reminiscent of a butterfly. This ignites curiosity: what might the symbolism or significance of this ‘butterfly shape’ truly be?

The Lorentz Attractor in all its Glory²
Let’s now take a glimpse at how these attractors change our estimates about the predictability of a system. You may be able to see how endogenous events of uncertainty emerge dependent on where your path is located on this attractor. The path dependent structure influences the uncertainty of our trajectory dependent on not only the initial state, but also where it is located on the path of allowable states.

From Predictability to Chaos²
Top Left Scenario: If the initial ring of uncertainty remains unchanged, it means our initial uncertainty about the system’s state has not grown. Essentially, our initial guess about the system’s state remains as uncertain (or certain) as before.
Top Right Scenario: Here, the ring becomes a “banana/boomerang” shape. This indicates that as the system evolved, the uncertainty regarding its state has changed in a specific manner. The transformation into a thin shape suggests that we’re not sure if the system will transition from one state (represented by the left-hand lobe) to another (the right-hand lobe).
Bottom Figure: In this scenario, there’s a high degree of uncertainty regarding the future state of the system. The position on the attractor is very uncertain, meaning it’s hard to predict where the system will end up over time.
Complex adaptive systems underscore the profound significance of their historical trajectories in influencing our capability to anticipate future outcomes. These systems, with their intricate and sometimes elusive characteristics, vacillate between predictability and unpredictability throughout their existence. We can’t merely rely on straightforward ergodic statistics in such contexts. For price followers and others navigating these systems, the path taken is not just a record of the past but a crucial determinant of future possibilities. It is essential to recognize and respect the inherent complexities and path dependence of such systems when making decisions about risk. Expectations are for those who like to assume ergodicity. Be non-ergodic my friends and capitalise on this weakness.
Trade well and Prosper.
Footnotes:
- The Ergodicity Problem in Economics, Ole Peters, Nature Physics Published 02 December 2019
- The Primacy of Doubt, Tim Palmer, Oxford University Press, Published in 2022